原理说明
反激电源可以看作是Buck-Boost电路的一种,其输入、输出、开关占空比的关系与Buck-Boost电路是一样的,简化原理如下所示。
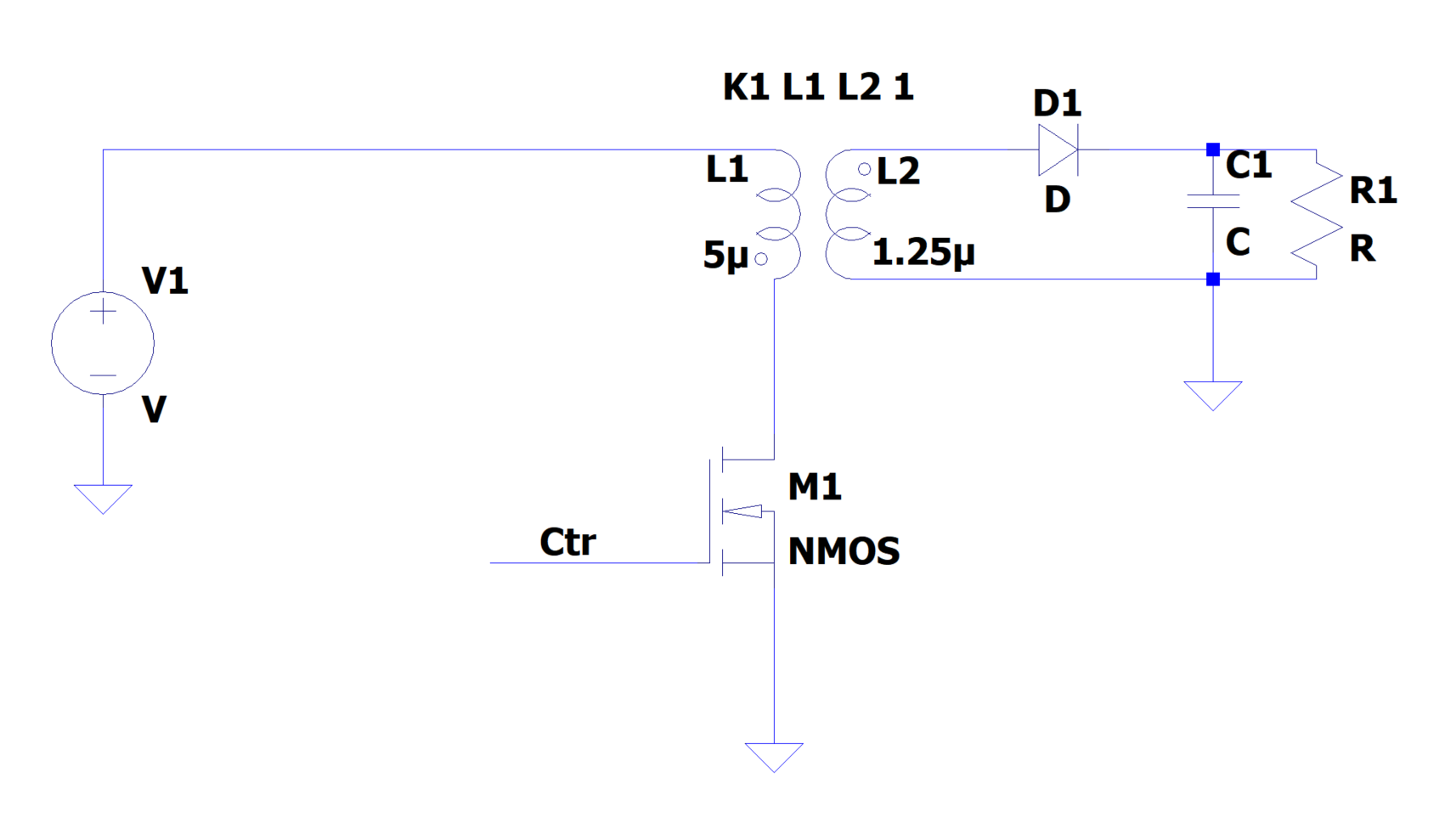
$Ctl$为开关信号,我图示使用的是nMOS,因此$Ctl$为高电平时nMOS导通,此时外部电源V1给变压器原边进行充电。变压器原边电压上正下负,变压器副边电压也是下正上负(注意变压器同名端子的位置),因此副边D1截止,这意味着副边不会有电流流过。$Ctl$为低电平时nMOS关断,变压器原边所存储的能量通磁场耦合到副边,D1正偏,原边所存储的能量通过D1给负载和电容进行供电。在整个系统达到稳态时,系统在一个开关周期开始和下一个周期开关的开始的状态是一致的。
给原理图加一点细节
实际上所有的器件都不是理想器件,变压器无论原边还是副边都存在漏感、二极管的PN结之间存在寄生电容、开关管的$Ciss$和$Coss$、实际生产安装引入的寄生电容和寄生电感等都会对系统工作产生很大的影响。为了避免过于繁琐的说明,考虑到实际影响的大小,这里仅考虑开关管的输出电容$Coss$、二极管的$Cj$。开关管的输出电容和二极管的$Cj$隐含在spice模型中,此处不再单独画出,最终的原理图如下所示。
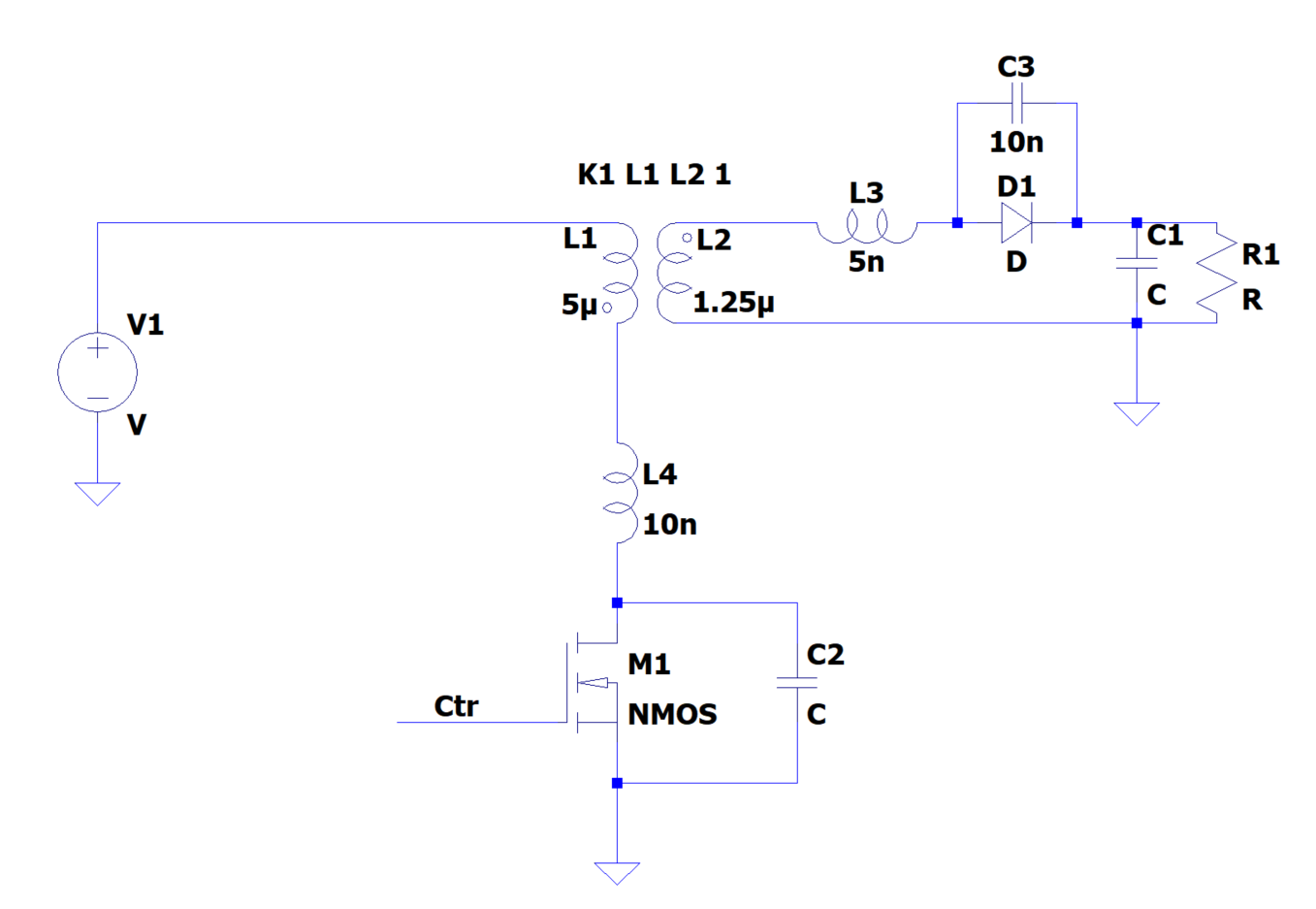
波形仿真
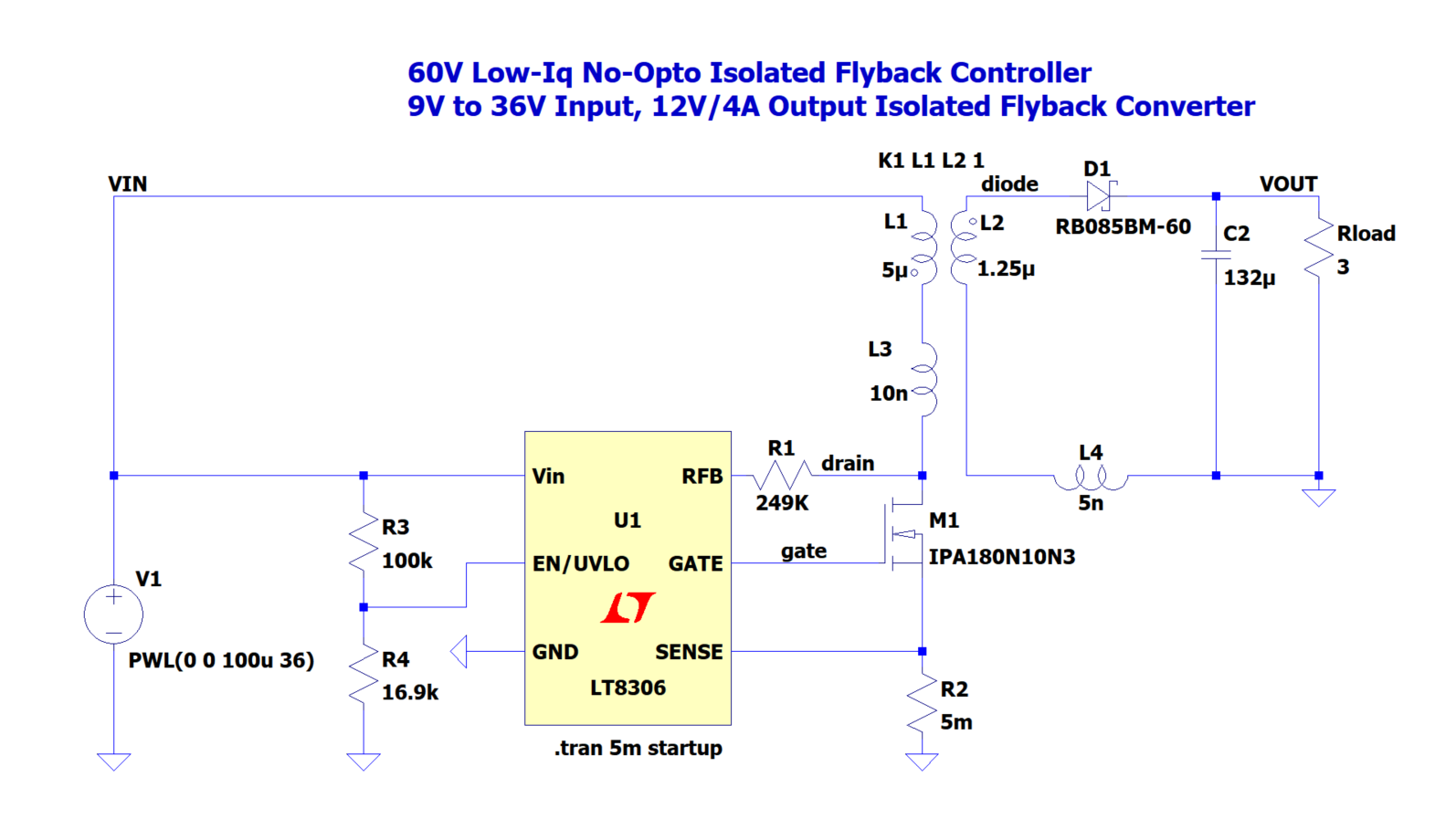
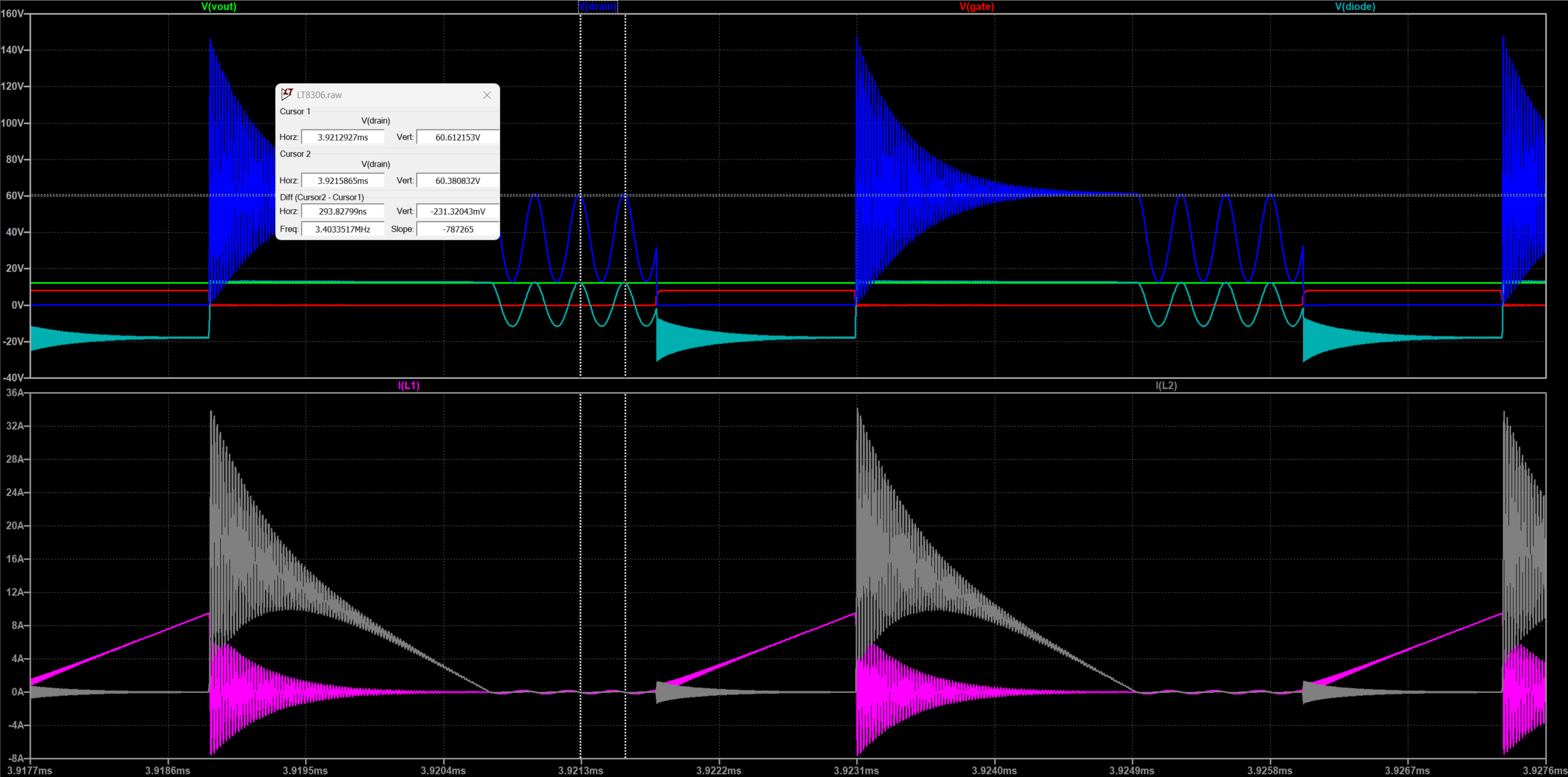
为了方便仿真,我使用LTspice的LT8306示意demo来做演示说明。LT8306是ADI的隔离反激电源控制器,在轻载时工作在DCM模式下,在重载时系统会启用准谐振控制器。demo默认使用的是3欧姆负载,LT8306demo原理图和仿真波形如下所示。
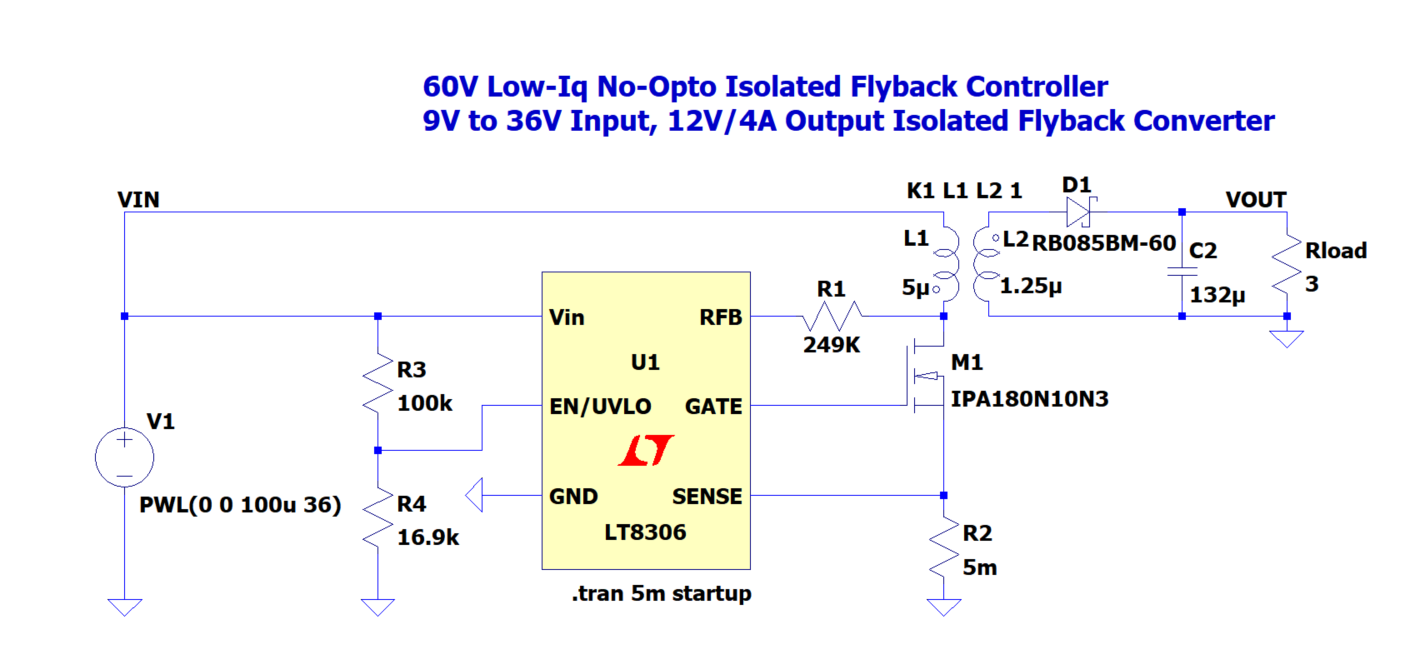
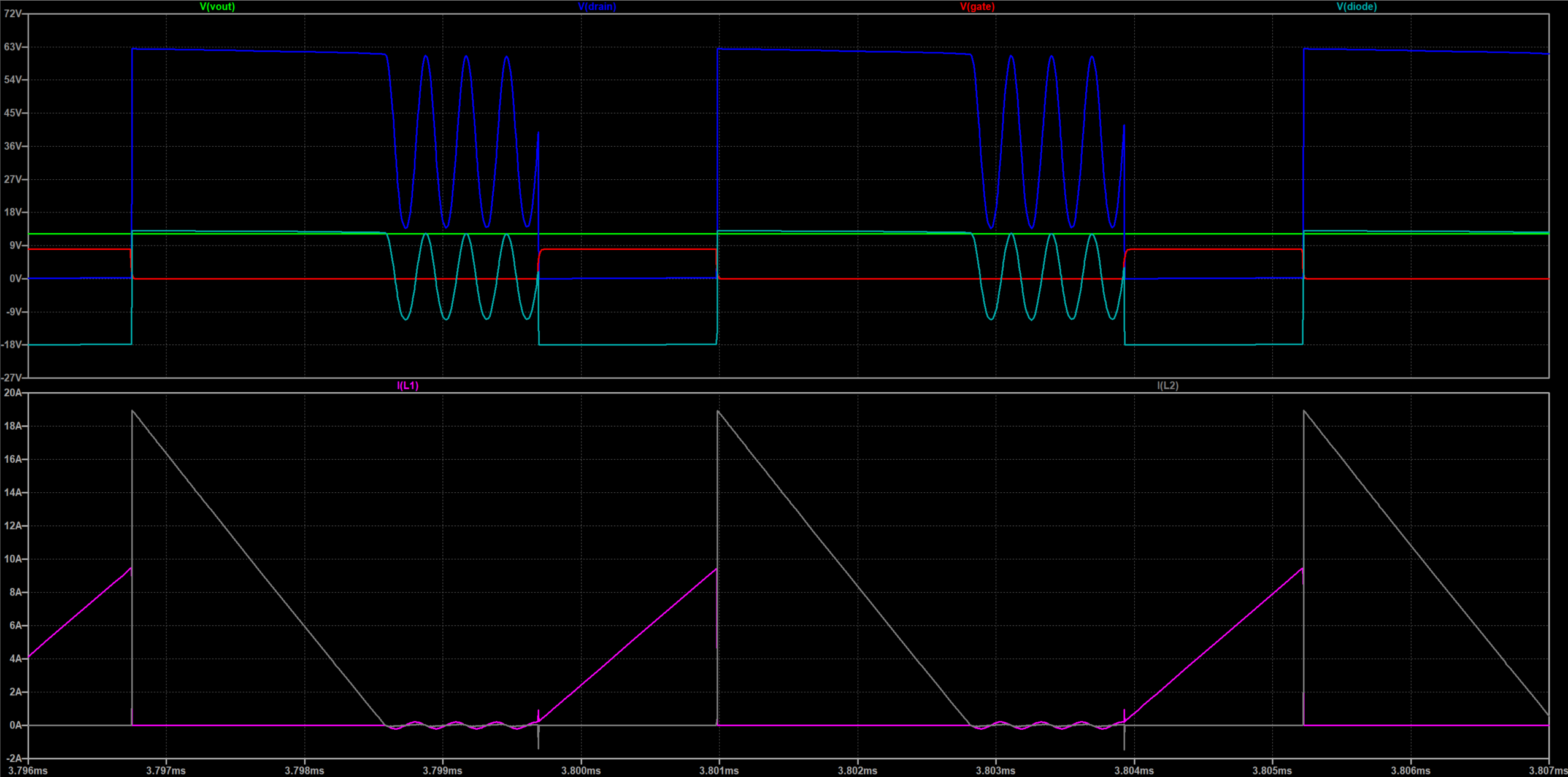
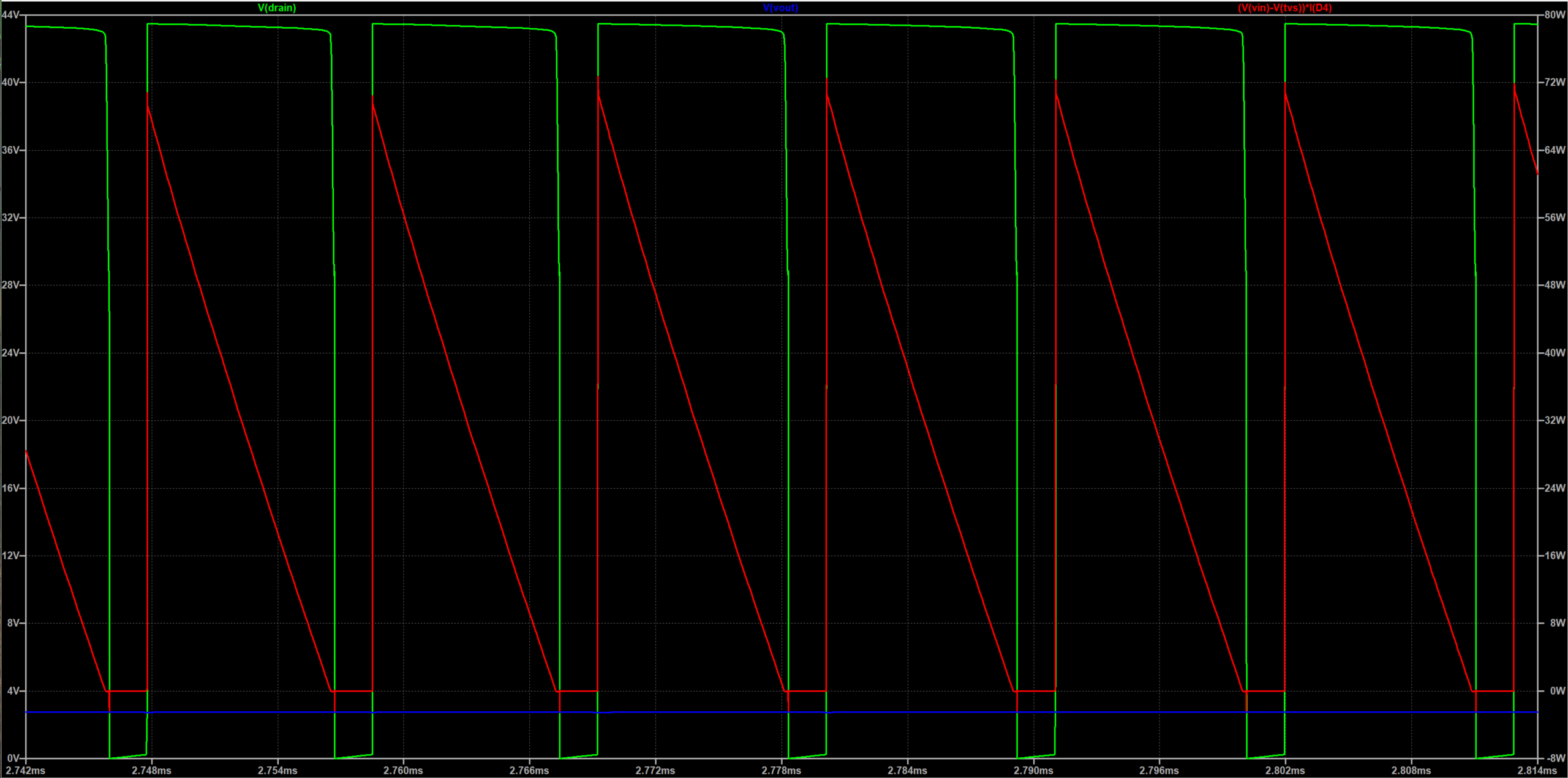
从图中可以看到,当gate管脚拉高到8V时,开始给变压器原边充电,电流$I(L2)$以固定速率逐渐上升。当gate管脚为0V时,变压器原边电流迅速下降为0,与此同时变压器副边的电流$I(L2)$突然增加,然后以固定速率下降。$Vin$电压为恒定的36V,而输出也为固定的12V。但是从图中可以发现$V(drain)$的电压在MOS关断期间,先升高至62V,然后缓慢下降直到副边电流降至0V,在此之后$V(drain)$会在62V到13V之间震荡。而在MOS开通期间,变压器副边的$V(diode)$会跌至-18V左右。
一点计算说明(理想状态下电压电流特性)
变压器的原副边线圈比N=2(原副边感值比开根号),从波形图可以看出$D={1.3\over3.1}=0.42$(工作在DCM模式),因此在输入电压为36V的情况下$Vout={36 \over N}\times {D \over (1-D)}-Vj=12V$。当MOS关断的时候,变压器原边的电压被副边电压钳位至${N \times (Vout+Vj)}=26V$,而且此时的原边上负下正,因此$V(drain)=36+26=62V$。当MOS打开时,变压器原边的压差为36V,这时通过变压器耦合到副边且副边上负下正,所以$V(diode)=0-{Vin \over N}=-18V$。当副边电流降至0时,原边的磁能由于没有别的泄放路径,只能和MOS的输出电容之间进行充放电,并持续震荡。从波形图中可以看出在$V(drain)$降低至$V(vin)$的过程中,变压器原边给nMOS的输出电容进行充电,原边存储的能量转移到了电容上。当原边的压差降为0V时,能量开始从nMOS的输出电容转移到变压器原边。由于电容和电感是储能器件,当损耗比较小时,系统会持续震荡,震荡的峰峰值即为(${(V(drain)-V(vin))\over 2} =56V$(这个电压刚好也是${(V(out)+Vj)\times 2N}$)。由于原边在震荡,且副边的$Cj$存在,因此即使是副边续流二极管反偏,原边的变压器震荡仍能耦合到副边上,且电压比例恒为$N$。
再给原理图加一点点细节
实际上变压器无论原边还是副边都存在漏磁的情况,磁场能量无法完全耦合到磁芯传导到另外一侧。在原理图的变压器加上漏磁电感,原理图和仿真波形图如下所示。
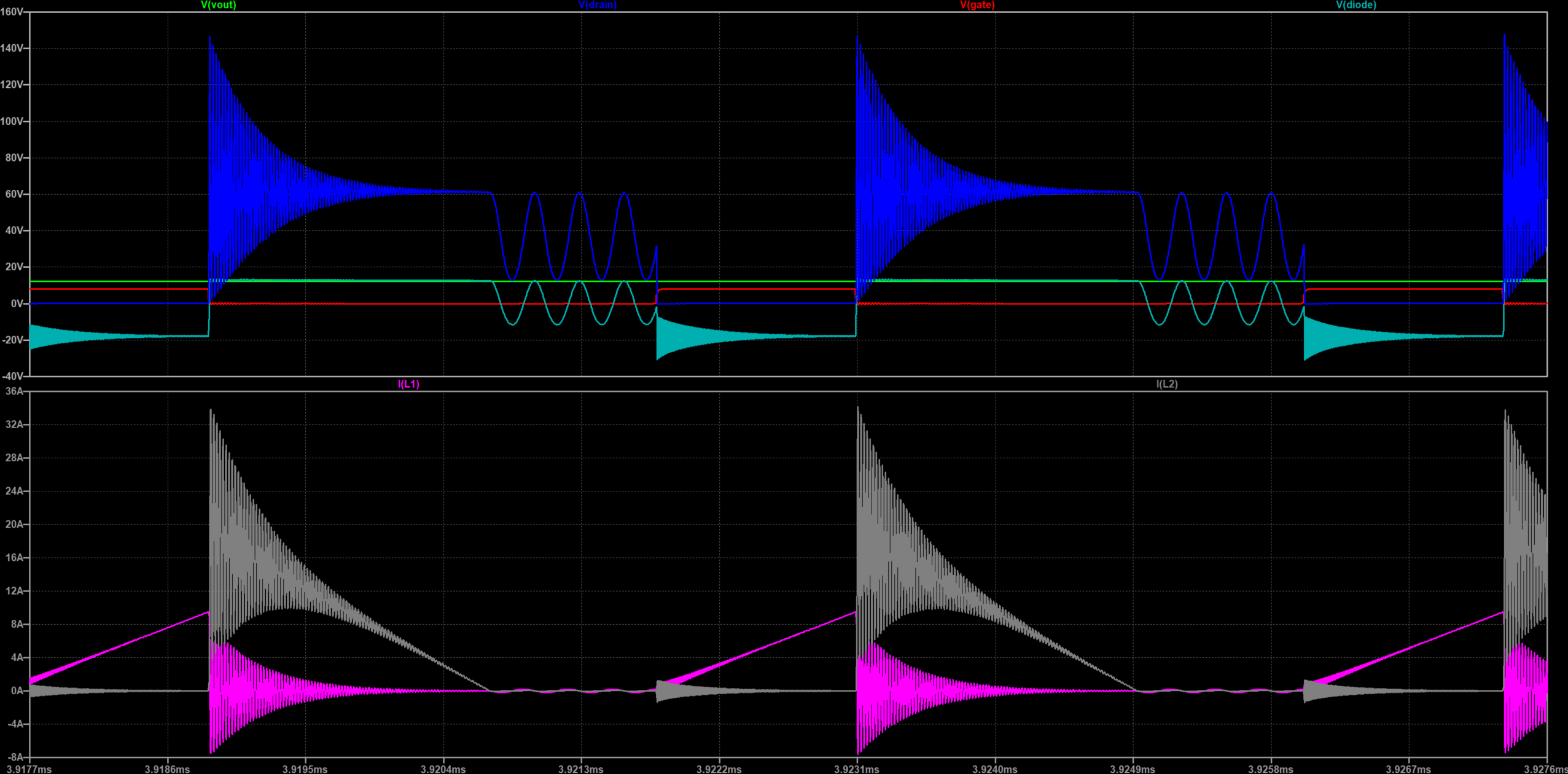
从图中可以看出,加了漏感之后,波形相较于之前发生了非常多的高频震荡。这些震荡的峰值电压可能会超过开关管的VDS反向耐压值,也有可能超过续流二极管的反向耐压值,进而损坏元器件。此外高频震荡也是辐射超标的一个重要原因。
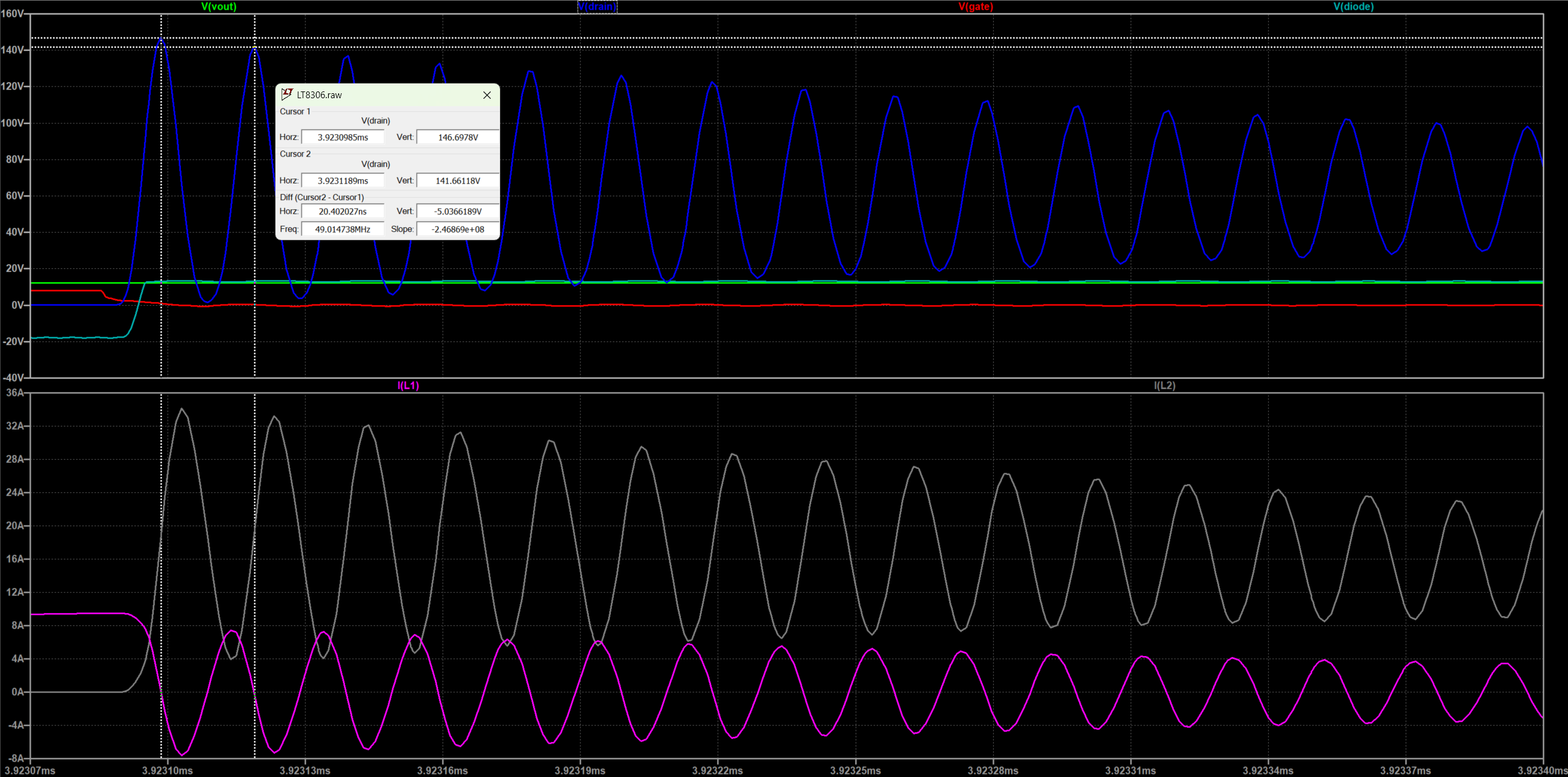
从波形图中不难看出,其实所有波形的整体趋势跟之前是一致的。当MOS关断时,变压器在给副边提供能量的同时,漏磁L3也会在M1的输出电容之间震荡,震荡产生的电压叠加副边的钳位电压以及供电电源的电亚已经达到了140V,是之前的两倍还多。
再来一点点计算(引入漏感之后的谐振频率)
在开关管打开时,电源给变压器原边和漏感进行充电,从图中可以看出最终流过原边和漏感的电流为9.5A。当开关管关断的时候,原边由于电磁耦合给副边供电,但是漏感的电流只能流进MOS的输出电容。我这里设计漏感$Lleak=10nH$,MOS管查其对应的$Coss$在$0.18nF \thicksim 1.5nF$之间(随着$Vds$的增大而减小)。为了验证结果的正确性,我反推计算$Coss$大小。关断后漏感两端的电压为下正上负,$V(leak)=9.5\times6.6=V$,$V(leak)=V(drain)-Vin+(Vout+Vj)\times N=58V$,因此计算$Coss={Lleak \over {(58 \div 9.5)}^2}=0.628nF$,在Coss范围之内。另外从图示可以看出在开关管关断后的短时间内V(drain)以49.0MHz频率震荡,根据谐振频率计算$Coss=1.06nF$,也在$Coss$范围之内。当副边的电流放完之后,续流二极管反偏,这时原边存储的能量联合漏感跟$Coss$谐振,根据谐振频率3.4MHz可以算出此时$Coss=0.44nF$。
尖峰电压与漏感、峰值电流、$Coss$之间的关系
$$E(Lleak)={1\over2} \times L(leak)\times I(peak)^2$$
$$E(Coss)={1\over2} \times Coss\times V(peak)^2$$
$$V(peak)=I(peak)\times {\sqrt{L(leak) \over Coss}}$$
尖峰吸收电路
开关管关断的时候,尖峰电压过高的的话可能会导致$V(drain)$电压超过$V(DS)$所允许的电压,因此需要加尖峰吸收电路。实际上漏感引起的峰值电压与漏感大小、$Coss$ 、原边峰值电流相关。漏感越小、峰值电流越小、开关管的输出电容越大尖峰电压越小。常见的措施有RCD电路、三绕组吸收电路、二极管钳位电路等,下面逐一介绍。
RCD吸收电路
RCD(电阻、电容、二极管)中电阻和电容的作用是用来钳位高频震荡的电压,为了避免对初级变压器充电的影响,添加二极管用来阻断旁路充电电流。原理图如下所示,下面详细分析整个过程。
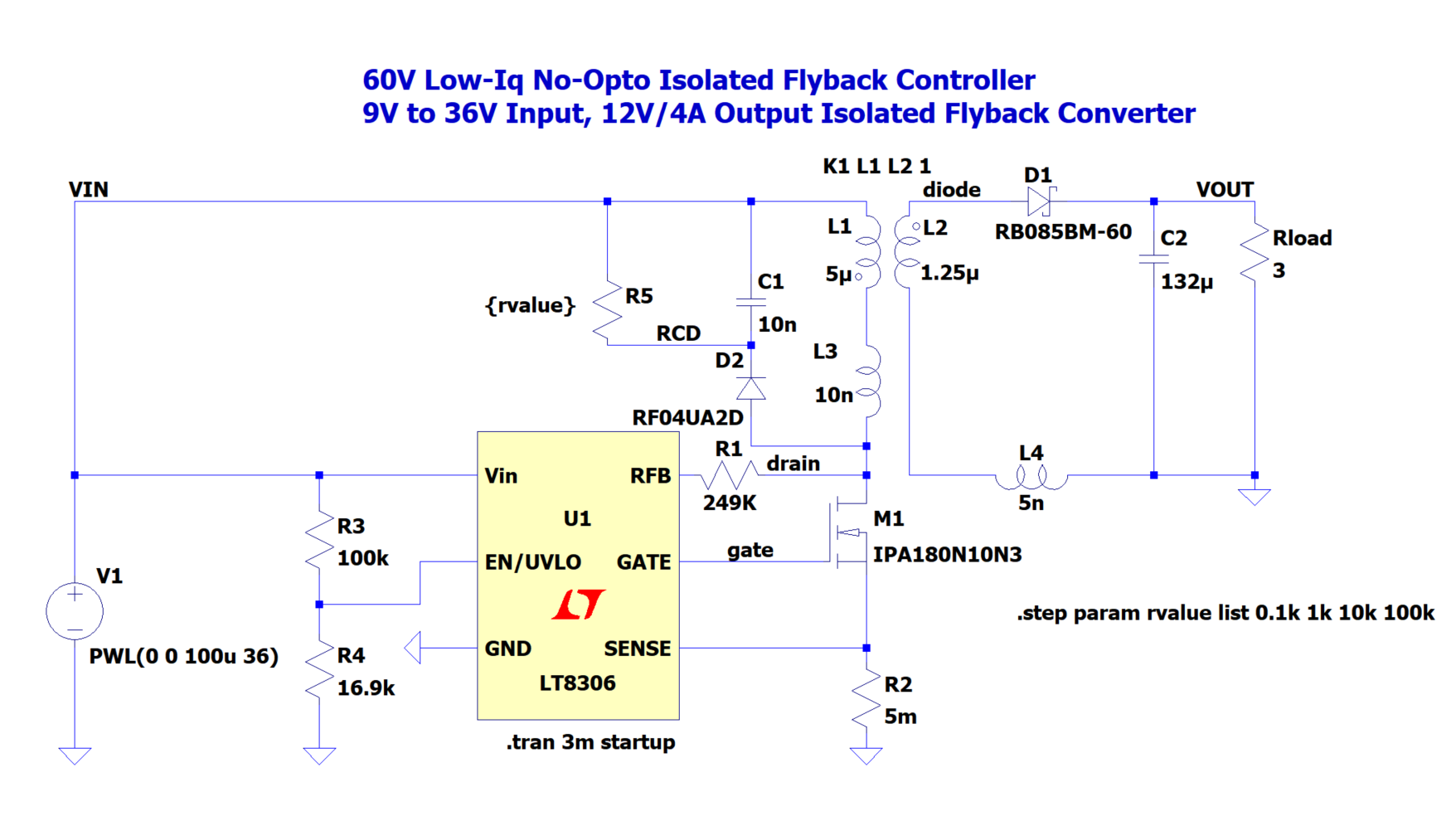
随着$V(drain)$电压的升高,$D2$逐渐正偏,电流流过$D2$给电容充电(电容相对于电阻来说阻抗比较低,因此大部分电流都流入电容$C1$,另外还有部分电流流入$Coss$,两个电容的分流比例取决于容值的大小,我图示中$C1=10nF$是$Coss$的10倍左右)。$C1$两端的压差逐渐增大,直到$V(drain)-V(RCD)<Vj(D2)$,因此实际上$V(drain)$电压被$C1$和$R5$钳位。只要$R5$足够小或者是$C1$足够大,就可以将$V(RCD)$电位限制到比较低,最终会限制$V(drain)$电位。将$R5$的阻值设置为$0.1K、1K、10k、100K$进行仿真,结果如下所示。从图中可以看出随着阻值的减小(电阻上消耗的功耗增加),钳位电压也在逐渐下降。
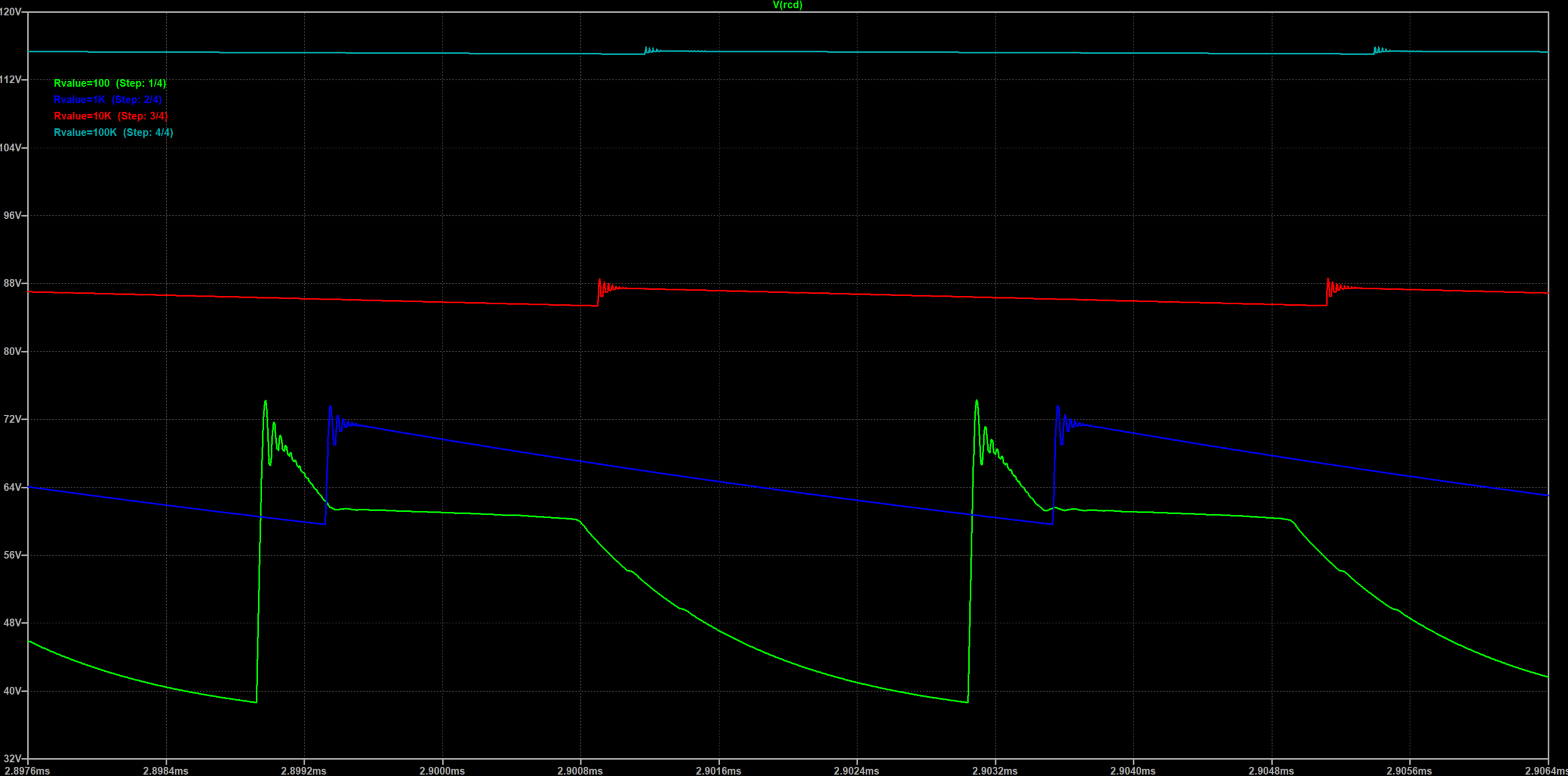
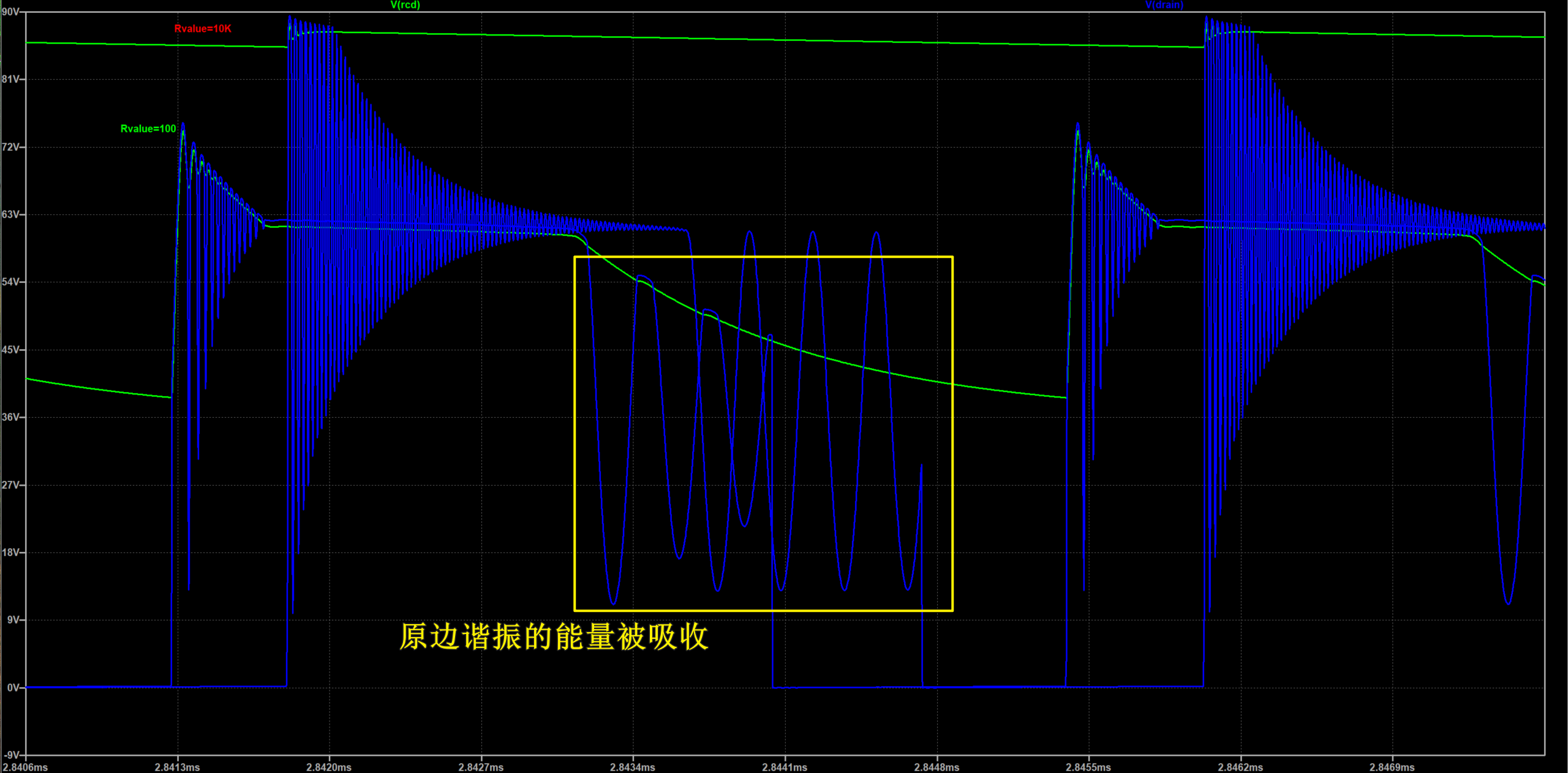
需要注意的是,随着$R5$的减小,在副边电流降至零点原边变压器与$Coss$谐振的电压也可能差也可能超过$Vj(D2)$,这导致过多的能量被$R5$吸收。下图为$V(RCD)$和$V(drain)$在$R5=100$和$R5=10K$下的波形。
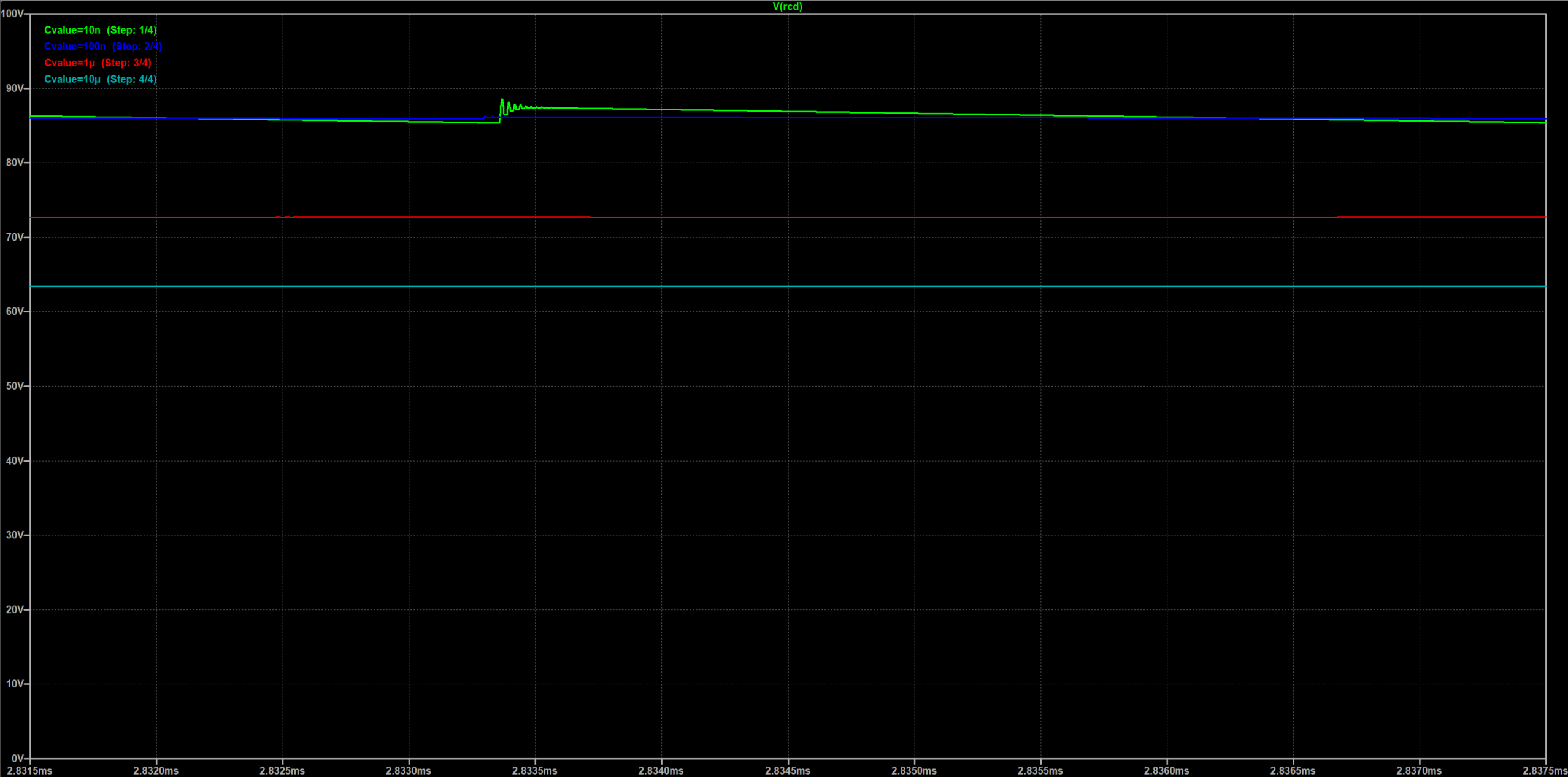
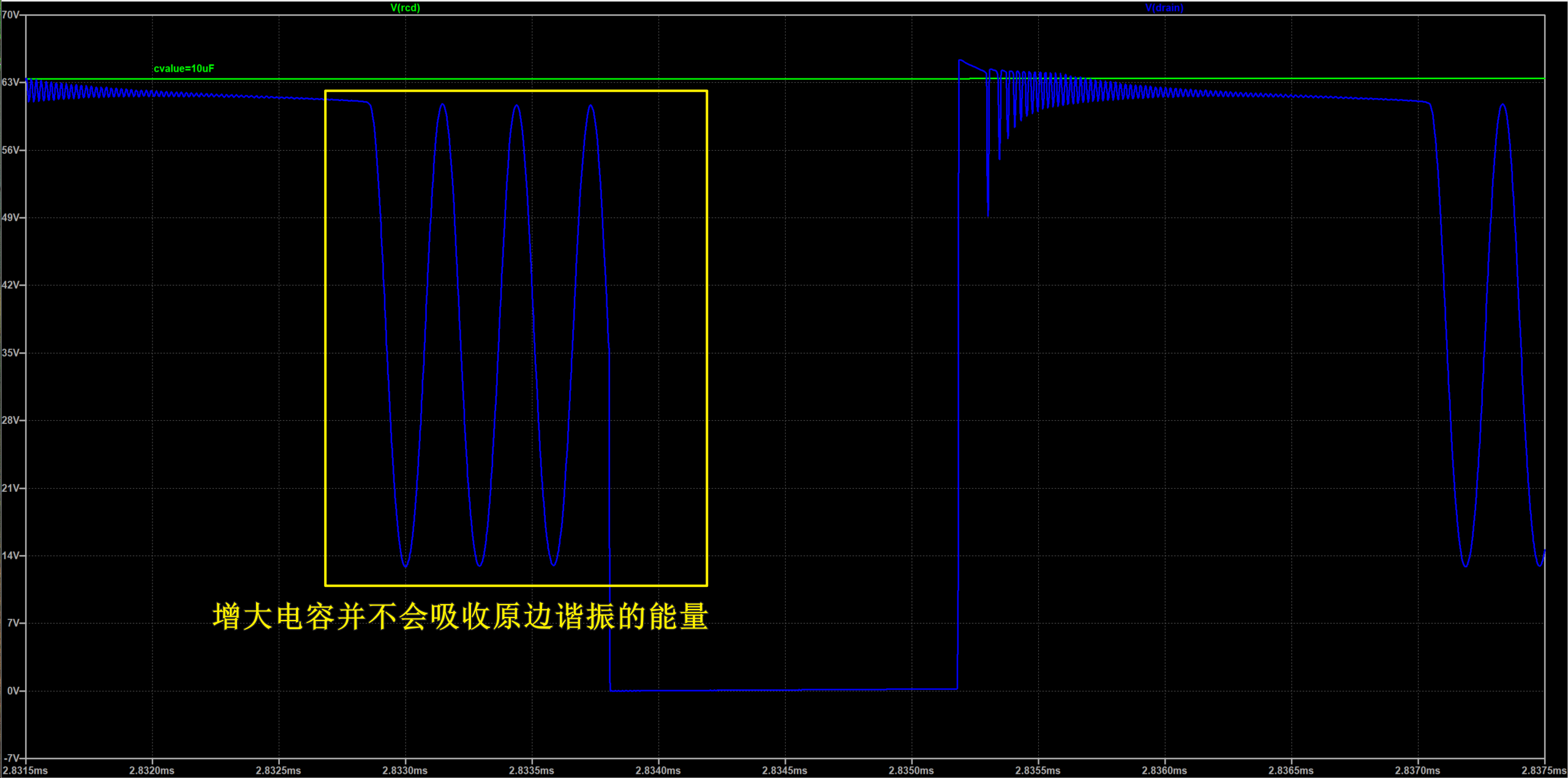
保持$R5$不变,修改C的容值分别为$10nF、100nF、1uF、10uF$,仿真结果如下所示。从结果可以看出随着容值的增加,RC将电压钳位的电压越小。
三绕组吸收电路
二极管钳位电路
利用TVS二极管的钳位功能,可以将漏感引起的尖峰电压迅速降低至钳位电压,为了避免影响初级线圈充电再加一个二极管。TVS二极管我选择的是SMCJ33A,其$V(so)=33V$允许功率为1.5KW,最大钳位电压为53.3V,原理如下所示。
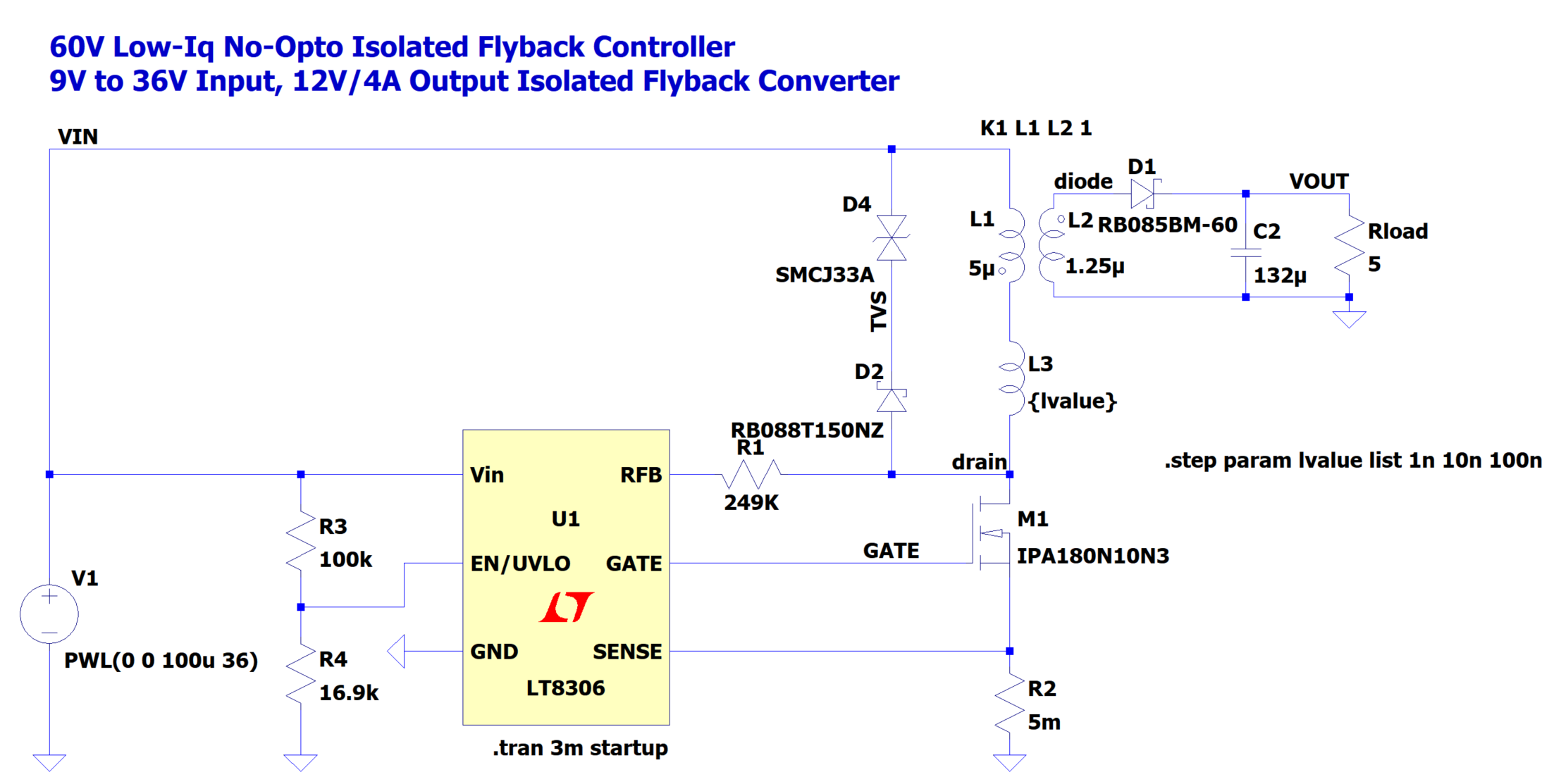
分别仿真漏感为$1nH、10nH、100nH$三种情况,抓取$V(drain)$及$D4$的功耗波形,结果如下。从图中可以看出随着漏感的增加,谐振峰值也会增加,但经过TVS二极管钳位之后可以大幅降低峰值电压。需要说明的是由于$D2$和$D4$的spice模型本身就含有$Cj$参数,因此峰值钳位电压会比预期更低。
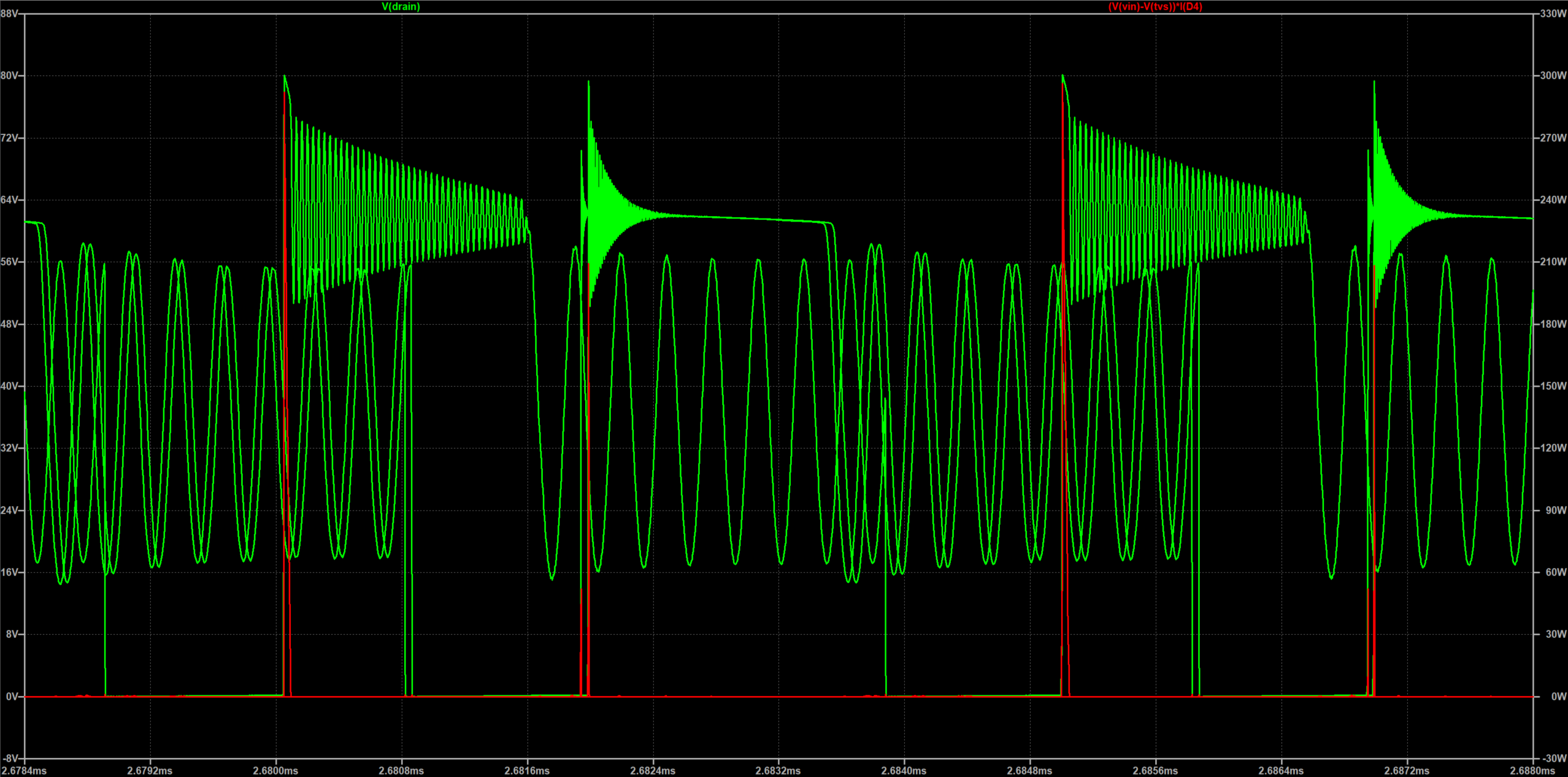
将波形展开之后可以看出峰值功率为300W左右,而且冲击时间远小于标称功率的测试模型,因此可以认为TVS二极管可以持续工作。
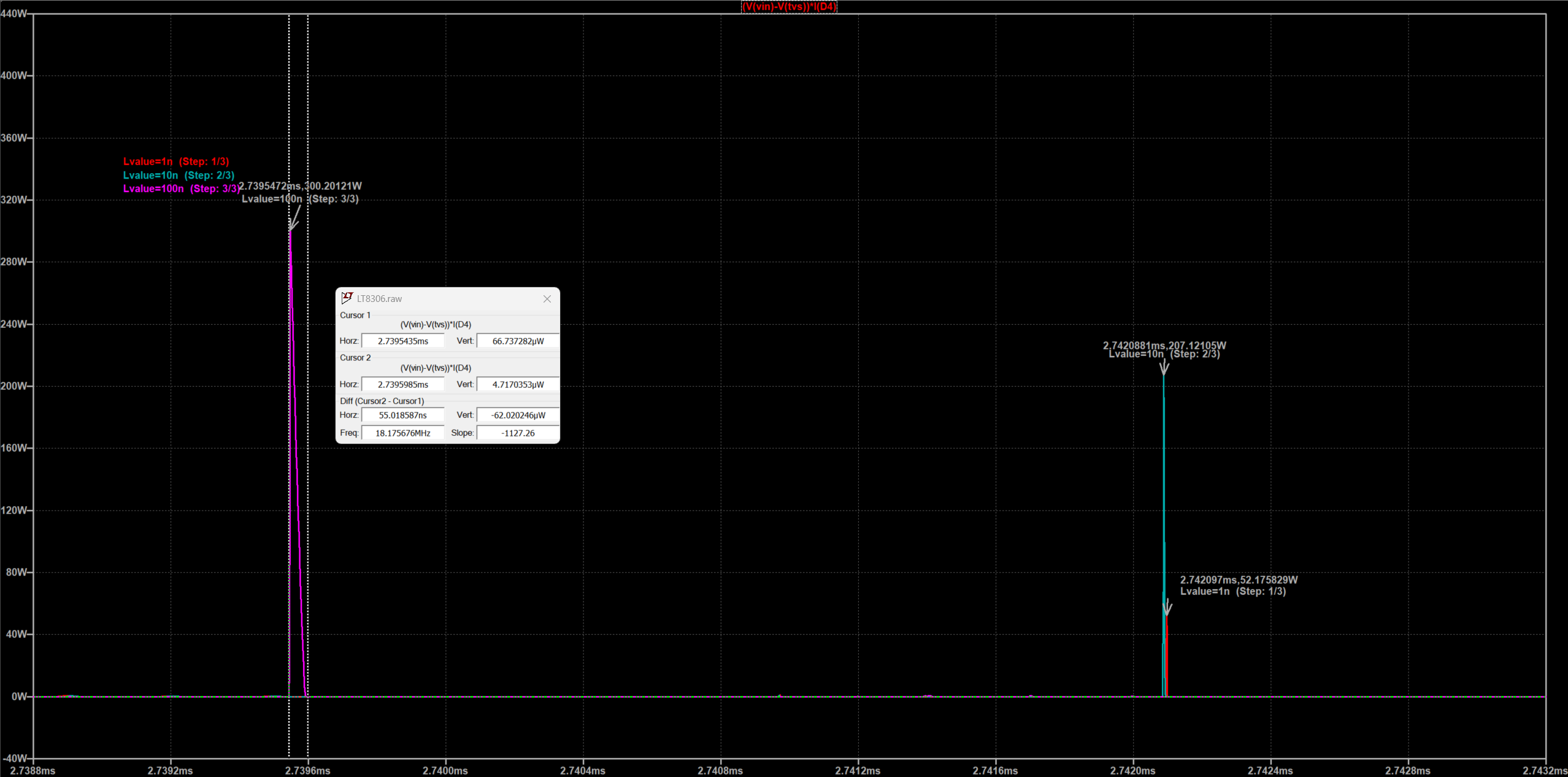
在设计时需要注意TVS二极管的功耗和钳位电压,如果钳位电压小于$(V(out)+Vj(D1))\times N + Vj(D2)$的话,会导致TVS长时间(即使峰值功率小于额定值,但是持续时间和频率远大于测试模型)处于钳位状态,这可能会损坏TVS二极管。另外由于变压器原边的压差也被TVS钳位,因此会导致无法输出足够的电压。下图为我选用了$SMDJ5.0CA$之后的仿真波形,可以看出$V(drain)=V(in)+V(clamp)+Vf(D2)=43.5V$,变压器两端的压差仅为7.5V,耦合到副边的电压再减去$Vf(D1)$就只有2.5V左右。
MOS的效率分析与计算
损耗分为静态损耗和开关损耗。静态损耗是指电路本身的静态电阻流经电流之后的损耗,比如MOS管的内阻$Rds(on)$、变压器的直流电阻、二极管的正向导通电阻等等。在LT8306的demo中使用了原边电流反馈,在原边的电流回路中添加了5毫欧的电阻。开关损耗一般是MOS管在开关的过程中$V(ds)$和$I(ds)$同时不为零时的损耗。下面以二极管钳位电路来分析开关管的损耗。
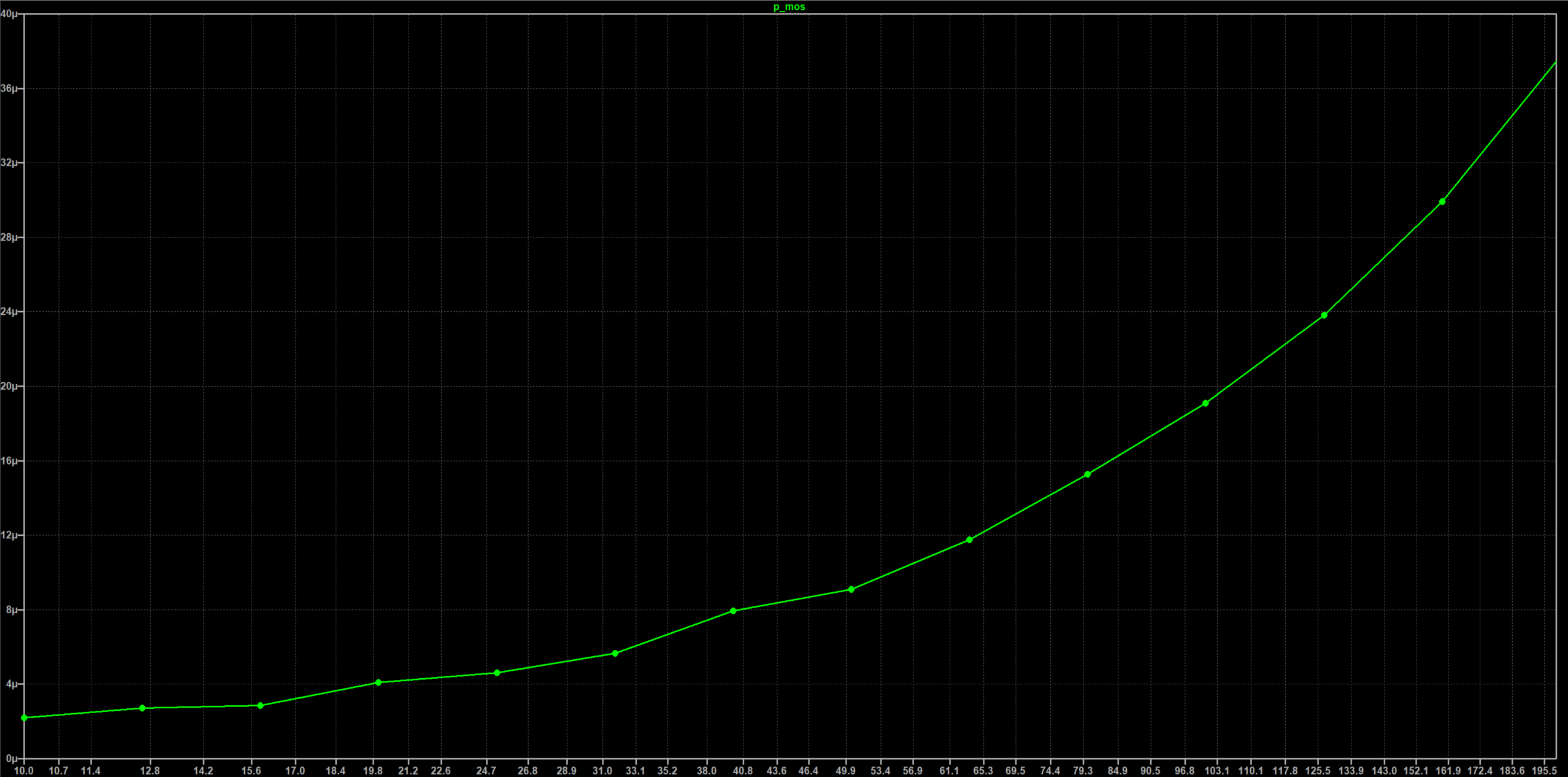
由于MOS的门极在开关的过程中无法提供足够大的驱动电流,密勒效应导致门极在爬升的过程中出现台阶,这会进一步延长开通时间,同样的关断的时候由于门极的寄生电容泄放路径的电流过小导致关断时间延长。将一个开关周期内MOS管漏极和源极之间电流和电压之积对时间的积分即为这个周期内产生的功耗,这个测试结果既包含了静态损耗又包含了开关损耗。设置不同的门极驱动电阻,结果如下。
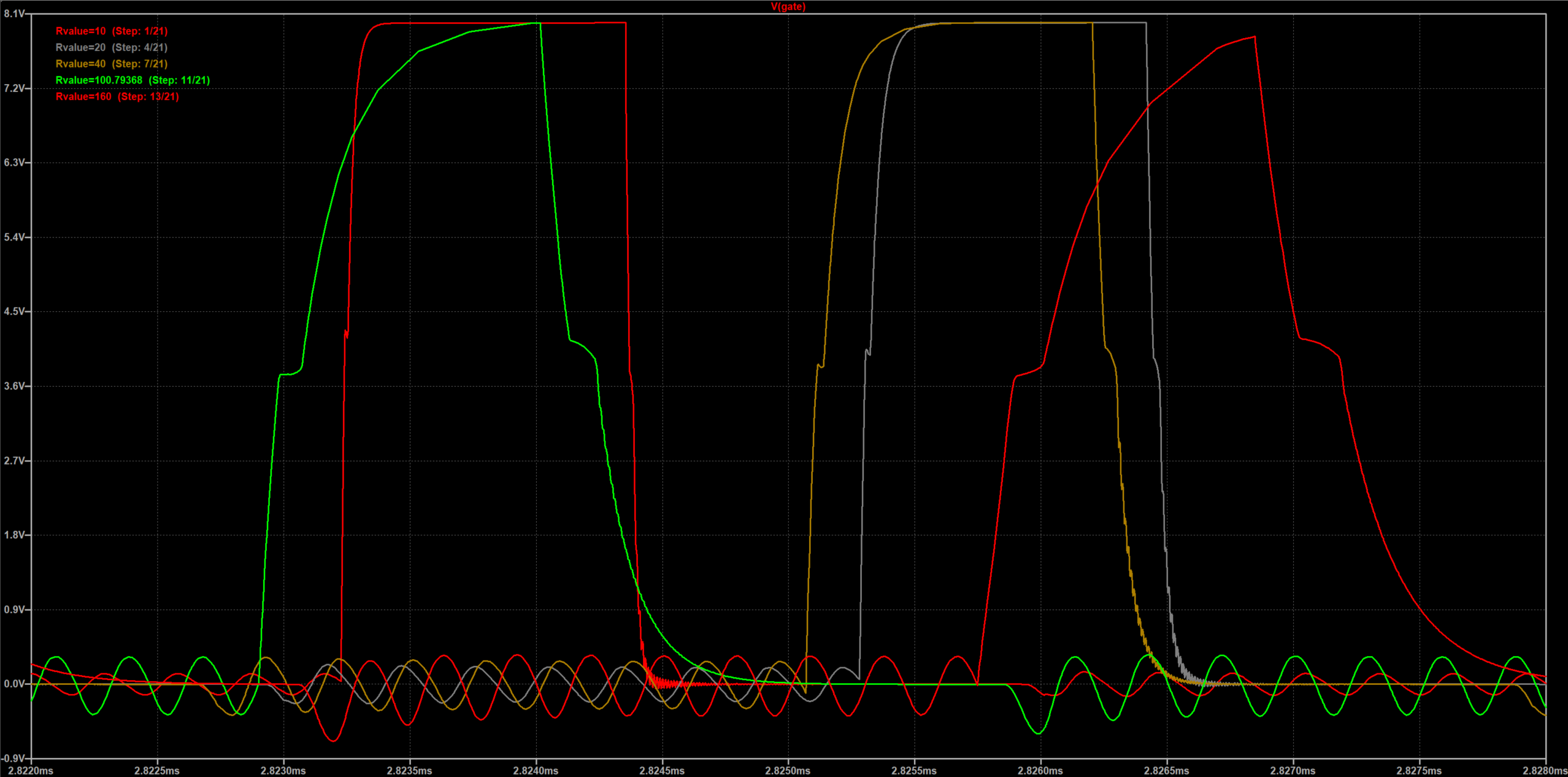
从图示可以看出随着电阻的增加MOS门级开通时间逐渐变长,MOS的损耗也逐渐增加。当驱动电阻达到160欧姆时,门极电压甚至都不能达到驱动电压。将160欧姆以内的电阻及功率采集数据整理成波形如下所示。从图中可以看出当驱动电阻达到160欧姆时在一个开关周期内的损耗为$30uW\over freq$,功率为$30\times10^{-6}\times200\times10^3=6W$。原理图中使用的nMOS型号为IPA180N10N3,其热阻为$5K/W$,因此温升为30度。